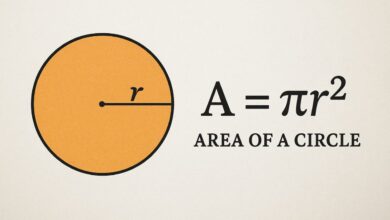
Understanding the Rsquared Circle in Mathematics
In the fascinating world of mathematics, the rsquared circle stands out as a fundamental concept that bridges geometry and everyday problem-solving. At its core, the rsquared circle refers to the geometric shape where the radius squared plays a pivotal role, particularly in calculating the area enclosed by the circle. This simple yet profound idea, often expressed through the formula involving πr², has intrigued mathematicians for centuries. Whether you’re a student exploring basic geometry or a professional applying math to real-world scenarios, grasping the rsquared circle opens doors to deeper insights.
The rsquared circle isn’t just a static shape; it’s dynamic in its applications. Imagine slicing a pizza or designing a wheel—the rsquared circle helps quantify the space within these circular forms. In this article, we’ll dive into the history, derivation, properties, and practical uses of the rsquared circle, ensuring you leave with a clear, comprehensive understanding. By the end, you’ll see why the rsquared circle remains a cornerstone of mathematical education and innovation.
The Historical Evolution of the Rsquared Circle
The concept of the rsquared circle traces its roots back to ancient civilizations, where early mathematicians grappled with measuring circular spaces. Around 250 BCE, the Greek scholar Archimedes made groundbreaking contributions by approximating the area of what we now call the rsquared circle. He used a method of inscribing and circumscribing polygons around a circle to squeeze closer to the true value of π, the constant that multiplies r squared in the area formula.
Archimedes’ work laid the foundation for understanding how the rsquared circle’s area relates to its radius. The Babylonians and Egyptians, even earlier around 2000 BCE, had rough estimates for circular areas, but they didn’t formalize the rsquared circle as precisely. It wasn’t until the Renaissance that European mathematicians like William Jones in 1706 popularized the symbol π for the circle constant, solidifying the rsquared circle’s formula as A = πr².
In the 17th century, Isaac Newton advanced the rsquared circle through calculus, providing a rigorous derivation that explained why the area scales with r squared. This historical progression shows how the rsquared circle evolved from intuitive approximations to a precise mathematical tool. Today, the rsquared circle influences fields from astronomy to engineering, proving its timeless relevance.
| Read More Related Post: the Power of Pi R Squared |
Deriving the Formula for the Rsquared Circle
Deriving the area of the rsquared circle is a delightful exercise in mathematical reasoning. Start with the basic idea: a circle is the limit of a polygon with infinitely many sides. By considering a regular polygon inscribed in the rsquared circle, we can sum the areas of tiny triangles formed from the center to each side.
Each triangle has a base approximately equal to the arc length and height equal to the radius r. As the number of sides increases, the total area approaches πr². Archimedes’ exhaustion method essentially does this without modern limits, bounding the rsquared circle’s area between polygonal approximations.
For a more modern approach using calculus, integrate the circumference elements. The area of the rsquared circle can be found by integrating (1/2)r² dθ from 0 to 2π, which simplifies to (1/2)r² * 2π = πr². This derivation highlights why the rsquared circle’s area is quadratic in the radius—doubling r quadruples the area, a key property.
Another intuitive way to derive the rsquared circle formula is through the relationship between area and circumference. The circumference C = 2πr, and since area builds up from infinitesimal rings, it integrates to πr². These methods ensure the rsquared circle’s formula is not just memorized but truly understood.
Key Properties of the Rsquared Circle
The rsquared circle exhibits several intriguing properties that make it indispensable in geometry. First and foremost, its area is always π times r squared, regardless of the circle’s position or orientation. This invariance under translation and rotation underscores the rsquared circle’s symmetry.
One notable property is the scaling effect: if you enlarge the rsquared circle by a factor k, the area multiplies by k². This is because r becomes kr, and (kr)² = k² r², so the rsquared circle’s area scales quadratically. In contrast, the circumference scales linearly, highlighting the difference between linear and areal dimensions.
The rsquared circle also relates to other shapes. For instance, the area of a sector of the rsquared circle is (θ/2π) * πr² = (θ/2) r², where θ is the central angle in radians. This fractional approach is useful for partial rsquared circles, like pie slices.
Moreover, in coordinate geometry, the equation of the rsquared circle centered at the origin is x² + y² = r², directly tying into the rsquared circle concept. These properties not only define the rsquared circle but also extend to advanced topics like complex numbers, where the rsquared circle represents points at a fixed modulus.
Applications of the Rsquared Circle in Mathematics and Beyond
The rsquared circle finds applications far beyond textbook problems, permeating various mathematical and practical domains. In pure mathematics, the rsquared circle is crucial for calculus, where it’s used to derive volumes of spheres via the method of disks—V = (4/3)πr³, building on the rsquared circle’s area.
In probability and statistics, the rsquared circle appears in uniform distributions over circular regions, helping model random points within a rsquared circle for simulations. For example, generating random numbers to fill a rsquared circle tests algorithms in computational geometry.
Engineering applications abound with the rsquared circle. In designing circular pipes, the cross-sectional area πr² determines flow rates, optimizing fluid dynamics. Automotive wheels rely on the rsquared circle to calculate tire contact patches, affecting grip and safety.
In physics, the rsquared circle models planetary orbits approximately, where gravitational potential involves r squared terms. Even in computer graphics, rendering shaded rsquared circles uses the area formula for pixel filling and anti-aliasing.
Agriculture benefits from the rsquared circle too—farmers use it to compute irrigation needs for circular fields. In architecture, domes and arches incorporate rsquared circle calculations for material estimates. These diverse applications demonstrate how the rsquared circle solves real-world challenges efficiently.
Furthermore, in data visualization, pie charts are segmented rsquared circles, proportional to data shares. This visual tool aids in business analytics, making complex info digestible. The rsquared circle’s versatility ensures its place in interdisciplinary studies, from biology (modeling cell membranes) to economics (circular flow models).
Advanced Insights into the Rsquared Circle
Delving deeper, the rsquared circle intersects with number theory through approximations of π. Infinite series like Leibniz’s formula converge to π, enabling precise rsquared circle computations for large r.
In non-Euclidean geometry, analogs to the rsquared circle exist, but in standard Euclidean space, it reigns supreme. Fractal geometry even explores self-similar rsquared circles, like in the Apollonian gasket, where nested circles fill space iteratively.
The rsquared circle also ties into optimization problems. For instance, minimizing material for a given volume leads to spherical shapes, rooted in rsquared circle integrals. These advanced insights reveal the rsquared circle’s depth, inviting further exploration.
Conclusion
The rsquared circle, with its elegant formula πr², encapsulates the beauty and utility of mathematics. From ancient derivations by Archimedes to modern applications in technology and science, the rsquared circle has shaped our understanding of space and quantity. Its properties of scaling and symmetry make it a versatile tool, while its historical evolution underscores human ingenuity.
As we’ve explored, the rsquared circle isn’t merely a formula—it’s a gateway to broader mathematical landscapes. Whether calculating areas for practical purposes or pondering theoretical implications, embracing the rsquared circle enhances problem-solving skills. In a world increasingly reliant on precise measurements, the rsquared circle remains an essential concept, promising continued relevance in education and innovation.
Frequently Asked Questions (FAQs)
What is the basic formula for the area of a rsquared circle?
The area of a rsquared circle is given by A = πr², where r is the radius. This formula multiplies pi by r squared to yield the enclosed space.
How does the rsquared circle differ from a regular circle?
A regular circle is the shape itself, but the rsquared circle emphasizes the mathematical role of r squared in its area calculation, highlighting the quadratic relationship.
Why is pi important in the rsquared circle formula?
Pi (π) is the constant ratio of a circle’s circumference to its diameter, approximately 3.14159. It scales the r squared term to accurately represent the rsquared circle’s area.
Can the rsquared circle be used in three dimensions?
Yes, extending the rsquared circle leads to the sphere’s surface area (4πr²) and volume ((4/3)πr³), applying r squared in volumetric contexts.
How accurate are approximations for the rsquared circle?
For most practical uses, π ≈ 3.14 suffices for rsquared circle calculations. For precision, use more digits like 3.1415926535 to minimize errors.
What real-life example illustrates the rsquared circle?
Baking a round cake: the rsquared circle formula helps determine batter volume by calculating the pan’s base area as πr² times height.
Is there a way to derive the rsquared circle without calculus?
Absolutely—Archimedes used polygonal approximations to bound the rsquared circle’s area, proving it approaches πr² as sides increase.
How does the rsquared circle apply to probability?
In Monte Carlo simulations, points are randomly placed inside a rsquared circle to estimate π by the ratio of hits within the boundary.
What happens if the radius of the rsquared circle is zero?
If r = 0, the rsquared circle degenerates to a point with area 0, as 0 squared times π equals zero.
Why does the area of the rsquared circle scale with r squared?
This quadratic scaling arises because area is two-dimensional; linear dimensions like radius square to fill the plane proportionally.